21. 장내채권 매매 3 (작성중)

이제 거의 끝났습니다. 더욱 더 알쏭달쏭한 두가지 개념만 익히시면 끝입니다. 

 

듀레이션(Duration)

채권용어로는 채권 투자자금의 평균 회수기간이라는 뜻으로 채권투자 시 현재가치 1원이 상환되는데 걸리는 평균기간을 의미합니다. 
실제 계산을 위한 공식은 아래와 같지만 그냥 그런가보다 하고 넘어가시면 될 것 같습니다. 

이 듀레이션을 처음 만든 사람의 이름을 따서 맥컬리 듀레이션(Macaulay Duration)이라고 하며 아래의 공식으로 계산이 가능합니다. 

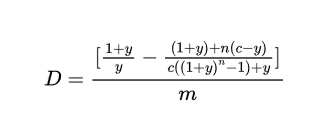
y : 1기간의 수익률, c : 1기간 기준의 표면금리, m : 연간 이자지급횟수, n : 만기와 연간 이자지급횟수의 곱

이 맥컬리 듀레이션을 이용해 채권가격의 변동위험을 계산하는 수정 듀레이션(MD: Modified Duration)또는 힉스 듀레이션(Hicks Duration)도 있습니다. 

듀레이션의 의미

이런 복잡한 계산식을 어째서 배워야 하냐면 몇 가지 장점이 있어서 그렇습니다. 

1. 듀레이션(맥컬리 듀레이션)을 계산하면 투자한 자금의 평균회수기간을 구할 수 있어 각기 다른 채권의 투자금 회수시기를 조절할 수 있습니다. 
2. 수정듀레이션을 사용하면 채권가격의 변동성(채권의 위험도)을 측정하는데 사용할 수 있습니다. 

조금 어렵게 느끼실 것 같아  추가 설명을 드리자면 듀레이션이라는 것은 결국, "돈을 회수하는데 걸리는 시간"이고 어떻게 보면 "만기까지 걸리는 시간"과 비슷하다고 할 수 있습니다. 그렇기 때문에 듀레이션이 길다는 의미는 채권의 투자자금의 회수시기가 오래 걸린다는 뜻이고, 이것은 시장의 금리변동에 의해 채권의 가치가 변화할 가능성이 높다는 의미이기도 합니다.

일반적으로 이 듀레이션(맥컬리 듀레이션)을 계산하면 각기 다른 채권의 투자금 회수시기를 일치시키는 채권 면역전략을 수립하여 내가 원하는 투자자금 회수시기에 모든 채권이 회수될 수 있도록 계획하는데 이용할 수 있습니다. 그리고 수정 듀레이션을 이용하면 어떤 채권이 만기까지의 시간이 길어 중간에 시중 금리의 영향을 많이 받는지 확인할 수 있습니다. 

많은 글에서 이 듀레이션이 채권에서 매우 중요하다고 설명을 하고 있습니다만 복잡한 계산식만 보여주며 채권 투자자들에게 무의미한 진입장벽만 높여준다는 생각을 개인적으로 하고 있습니다. 사실 굳이 계산을 하지 않아도 대충 느낌으로 알 수 있기 때문입니다. 
채권의 만기시기가 많이 남았다는 뜻(듀레이션이 길다는 의미와 거의 같습니다)은, 투자자금을 회수하는데 오래 걸린다는 뜻이며 시간이 길기 때문에 시중금리의 변화로 인해 채권의 가치가 변할 가능성이 높다는 뜻이니까요. 결국 시중금리가 가지고 있는 채권보다 올라가면 복잡한 듀레이션 계산을 하지 않아도 내 채권의 가치가 떨어지고 있다는 것을 알 수 있고 시중금리가 떨어지면 내 채권의 가치가 오르고 있다는 것을 느낄 수 있습니다.

결과적으로 이 듀레이션이라는 것은 각기다른 채권의 회수시기를 표준화해서 볼 수 있다는 것과 투자하는 채권의 가격변동 위험성을 표준화해서 보여준다는 것 이외에 큰 의미는 없다고 이해하셔도 딥니다. 물론 이것만으로도 매우 좋은 지표이지만 그 이상도 그 이하도 아니라는 말입니다. 그러니 듀레이션이 너무 어려워 전혀 모르겠다거나 계산을 못하겠다는 생각이 들어도 너무 두려워하지 마세요. 채권의 만기가 많이 남았으면 그냥 듀레이션이 긴 것입니다.

듀레이션의 계산

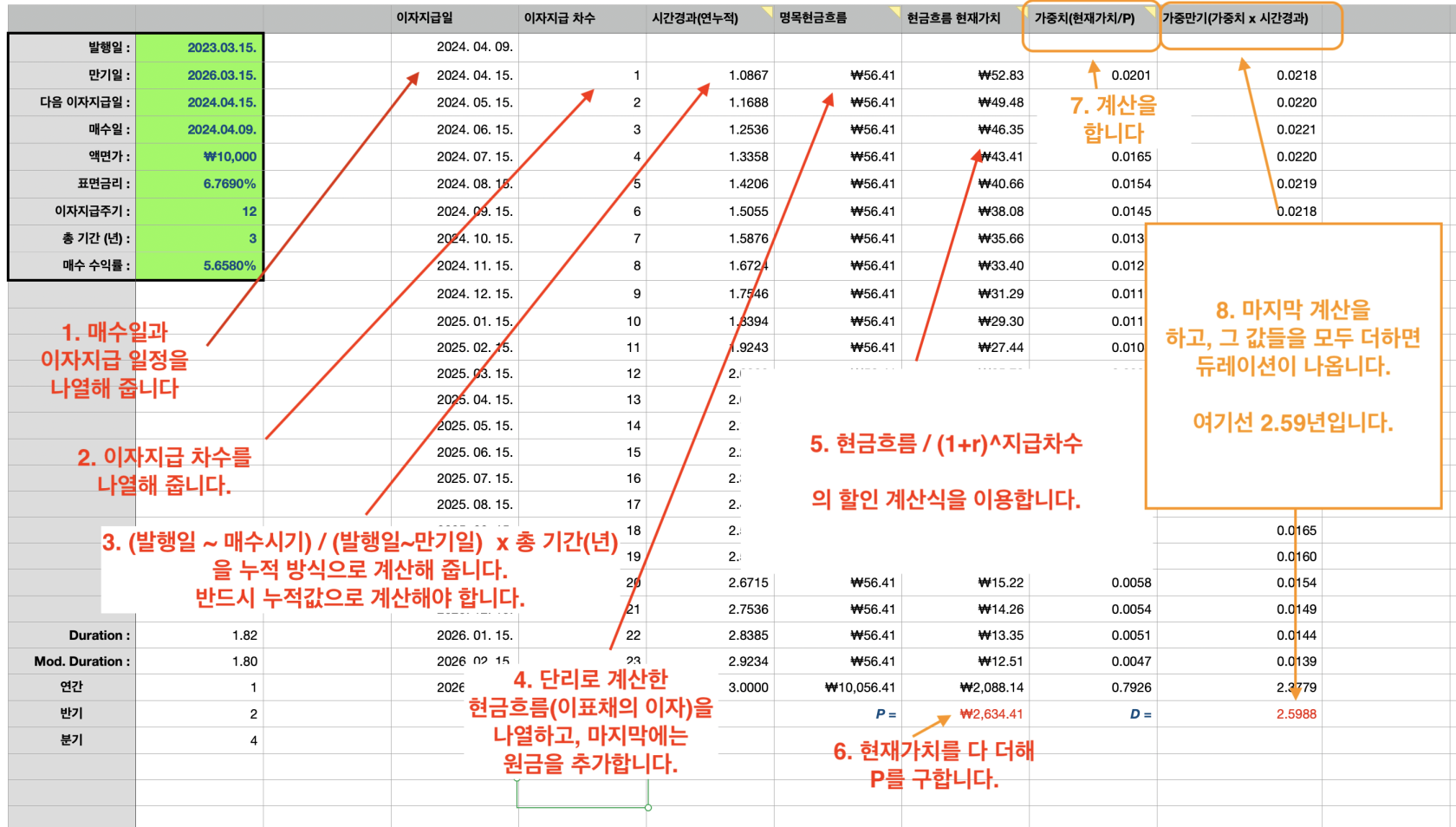
실제로 듀레이션을 계산하는 것은, 월이표채만 아니면 대부분 스프레드시트 프로그램에 이미 내장함수로 제공되어 있는 경우가 많습니다. 사용하는 사람이 거의 없다시피한 Apple의 Numbers에도 함수가 있을 정도니까요. 그렇기 때문에 대부분의 경우엔 그냥 프로그램에서 함수를 이용해 값을 확인하면 됩니다. 

보통 프로그램에서는 맥컬리 듀레이션과 수정 듀레이션의 두 가지 함수를 제공해주기 때문에 엉뚱한 것만 사용하지 않으시면 알아서 계산해 줍니다. 
단, 월이표채의 경우에는 사정이 다릅니다. 함수에서 매달 이자를 지급하는 월이표채를 지원하지 않는 경우에는 다음의 방식을 사용해서 계산해야 합니다. 

뭔가 머리가 아득해지는 내용이네요. 하지만 의외로 스프레드시트 프로그램을 사용하면 금방 구하실 수 있습니다. 

사실 듀레이션을 통해 알 수 있는 여러가지 채권가격의 변동에 대한 것도 있지만, 여기서는 생략하겠습니다. 상당히 현학적인 내용이고 실상은 우리보다는 학자들에게 어울리는 내용이라서요. 바로 다음으로 넘어가지요. 

채권의 볼록성(Convexity)

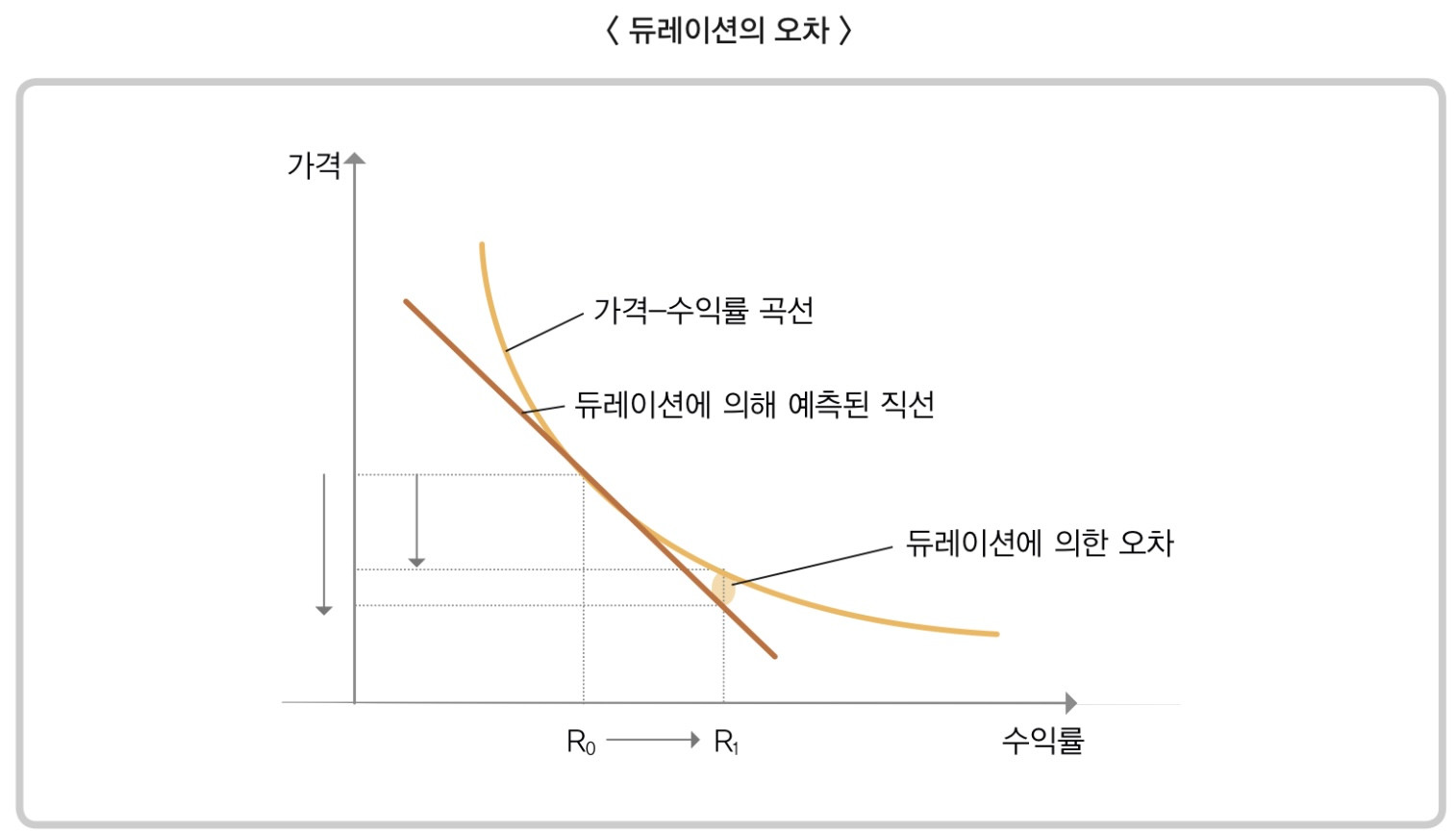
채권의 볼록성이란, 실제 듀레이션을 계산해 본 것과 달리 채권의 가격과 수익률의 그래프가 볼록하게 그려진다는 뜻입니다. 아래의 그림을 보시면 이해가 빠릅니다. 

이 그림의 곡선을 보시면 아시겠지만 채권의 수익률과 가격은, 수익률이 적으면 적을수록 (표면이율이 낮으면 낮을수록) 가격의 변동성이 커진다는 뜻이며, 수익률이 크면 클수록 (표면이율이 높으면 높을 수록) 가격의 변동성이 떨어진다는 것입니다. 계산상으로 보여지는 듀레이션 예측 직선과는 좀 다르게 움직인다는 뜻입니다. 

채권투자를 하는 우리의 입장에서는 그냥 그렇구나 정도만 이해하시면 되고, 실제로 필요한 부분은 채권을 적극적으로 사고 파는 경우에 이용됩니다. 

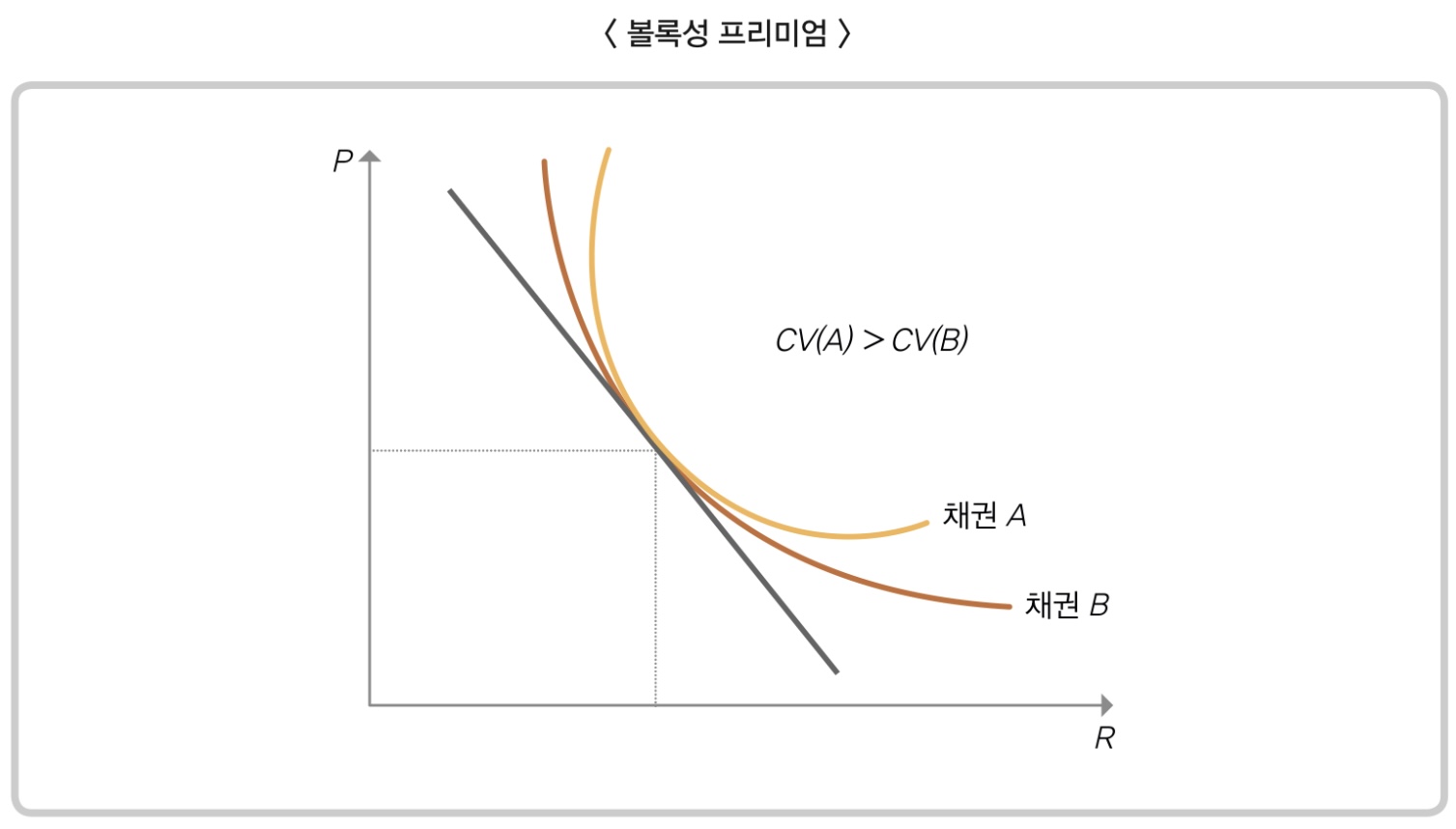
볼록성 프리미엄 

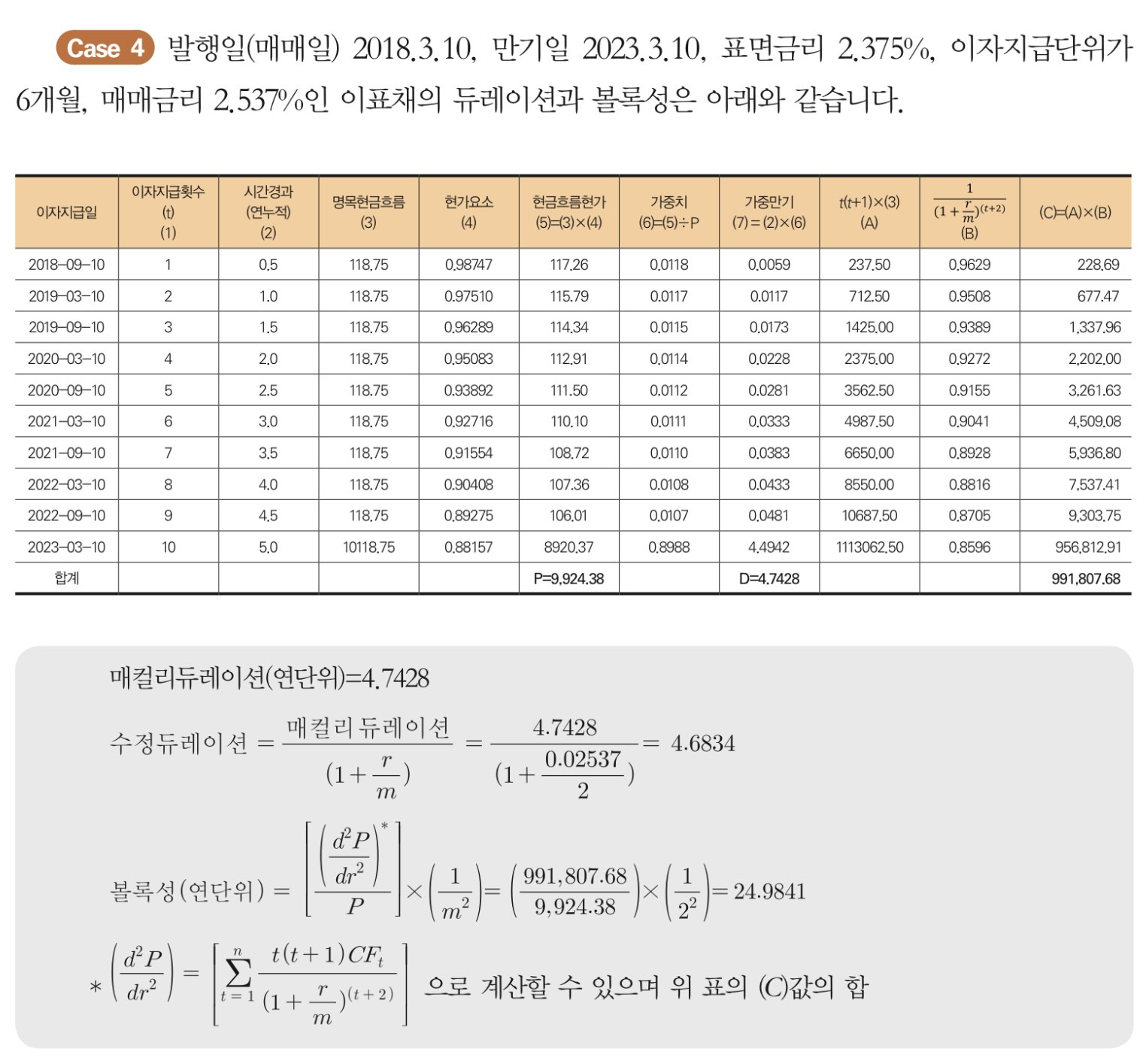
이 채권가치의 볼록성은 아래의 계산식으로 계산을 할 수 있습니다 : 

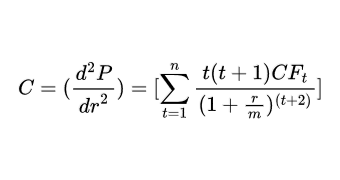
제가 공부한 책에서는 다음의 예제를 보여주고 있습니다. 이것을 보시면 이해가 쉬우실 것 같습니다. (계산하기 지쳐서...)

이러한 볼록성을 어렵게 계산까지 하면서 구하는 이유는, 볼록성 프리미엄 때문입니다. 아래의 그림을 보시겠습니다. 

채권 A와 채권B가 있을때, 일반적으로 수익률이 떨어지면 떨어질수록 볼록성이 큰 채권인 A의 가격이 높게 형성됩니다.
이것을 볼록성 프리미엄이라고 하며, 같은 듀레이션과 수익률을 가진 두 가지 채권이 존재할 때 볼록성이 큰 채권이 수익률 상승시기에 가격낙폭이 상대적으로 적고 수익률 하락시기에 가격낙폭이 상대적으로 크기 때문에 그렇습니다. 결국 채권의 볼록성이 크면 클 수록 같은 듀레이션과 수익률 상황에서는 더 가치가 있다고 이해하셔도 될 것 같습니다. 

일반적으로 시장변동성이 증가하면 볼록성 프리미엄은 증가하고, 안정적이면 볼록성 프리미엄은 감소합니다. 

실제 채권을 매수할 때 이 볼록성 프리미엄은 적극적인(Active) 투자자들에게는 매우 중요한 정보라고 생각합니다. 이들은 채권 자체의 이율보다는 채권거래를 통한 시세차익의 실현을 중시하니까요. 결국 볼록성에 대한 계산은 단순히 채권매수후 묵혀두기(Buy-and-hold) 전략을 취하거나 사다리 전략(Ladder Strategy)을 취하는 소극적(Passive) 투자자들에게는 큰 의미가 없을 수도 있습니다.